Class 8
In-Class Lab
Rethinking: Section 11.1.4
We’ll review the UCBadmit examples covered in Lecture 9.
library(rethinking)
data(UCBadmit)
d <- UCBadmit
d
## dept applicant.gender admit reject applications
## 1 A male 512 313 825
## 2 A female 89 19 108
## 3 B male 353 207 560
## 4 B female 17 8 25
## 5 C male 120 205 325
## 6 C female 202 391 593
## 7 D male 138 279 417
## 8 D female 131 244 375
## 9 E male 53 138 191
## 10 E female 94 299 393
## 11 F male 22 351 373
## 12 F female 24 317 341
It’s important to realize this data is on the aggregated level, not individual level. Because of this, we’ll use the (aggregated) Binomial model instead of a logistic model.
Initial Model
Let’s first plot our DAG.
library(dagitty)
g <- dagitty('dag {
bb="0,0,1,1"
G [pos="0.251,0.481"]
D [pos="0.251,0.352"]
A [pos="0.481,0.352"]
G -> D
G -> A
D -> A
}
')
plot(g)
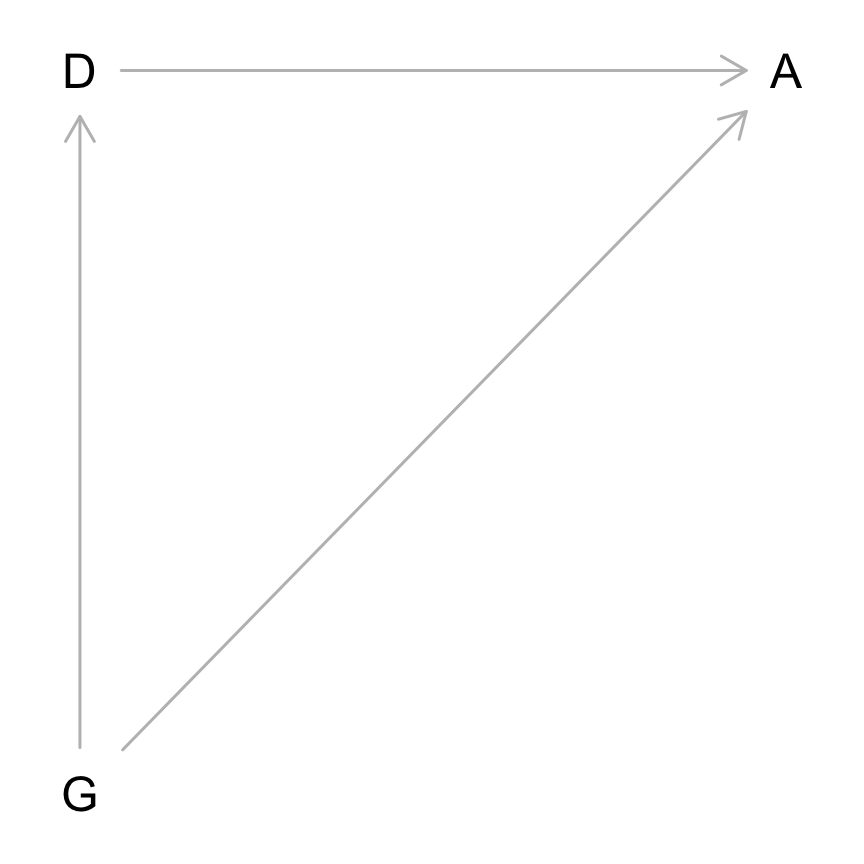
Since Department is a mediator, we would not condition by it to find the total causal effect of gender on admission.
For our model, we’ll need to create our dataset.
dat_list <- list(
A = as.integer(d$admit), # this variable is Admit in the book
N = as.integer(d$applications), # this variable is applications in the book
G = ifelse( d$applicant.gender=="male", 1L, 2L) # this is gid in book
)
We’ll also start with this initial model.
\(A_{i} \sim Binomial( N_{i},p_{i})\)
\(logit(p) = \alpha_{G[i]}\)
\(\alpha_{j} \sim Normal(0,1.5)\)
Prior Predictive Simulation
For this prior predictive simulation, we’ll use the extract.priors() function. To do this, we need to specify our model. Technically we’ll run the model but not analyse the model until the next step.
m11.7 <- ulam(
alist(
A ~ dbinom( N , p ) ,
logit(p) <- a[G] ,
a[G] ~ dnorm( 0 , 1.5 )
) , data = dat_list, chains = 4
)
## Running MCMC with 4 sequential chains, with 1 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 1 finished in 0.0 seconds.
## Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 2 finished in 0.0 seconds.
## Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 3 finished in 0.0 seconds.
## Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 4 finished in 0.0 seconds.
##
## All 4 chains finished successfully.
## Mean chain execution time: 0.0 seconds.
## Total execution time: 0.7 seconds.
Now we’ll run the prior predictive simulation.
set.seed(1999)
prior <- extract.prior(m11.7, n=1e4)
## Running MCMC with 1 chain, with 1 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 20000 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 20000 [ 0%] (Warmup)
## Chain 1 Iteration: 200 / 20000 [ 1%] (Warmup)
## Chain 1 Iteration: 300 / 20000 [ 1%] (Warmup)
## Chain 1 Iteration: 400 / 20000 [ 2%] (Warmup)
## Chain 1 Iteration: 500 / 20000 [ 2%] (Warmup)
## Chain 1 Iteration: 600 / 20000 [ 3%] (Warmup)
## Chain 1 Iteration: 700 / 20000 [ 3%] (Warmup)
## Chain 1 Iteration: 800 / 20000 [ 4%] (Warmup)
## Chain 1 Iteration: 900 / 20000 [ 4%] (Warmup)
## Chain 1 Iteration: 1000 / 20000 [ 5%] (Warmup)
## Chain 1 Iteration: 1100 / 20000 [ 5%] (Warmup)
## Chain 1 Iteration: 1200 / 20000 [ 6%] (Warmup)
## Chain 1 Iteration: 1300 / 20000 [ 6%] (Warmup)
## Chain 1 Iteration: 1400 / 20000 [ 7%] (Warmup)
## Chain 1 Iteration: 1500 / 20000 [ 7%] (Warmup)
## Chain 1 Iteration: 1600 / 20000 [ 8%] (Warmup)
## Chain 1 Iteration: 1700 / 20000 [ 8%] (Warmup)
## Chain 1 Iteration: 1800 / 20000 [ 9%] (Warmup)
## Chain 1 Iteration: 1900 / 20000 [ 9%] (Warmup)
## Chain 1 Iteration: 2000 / 20000 [ 10%] (Warmup)
## Chain 1 Iteration: 2100 / 20000 [ 10%] (Warmup)
## Chain 1 Iteration: 2200 / 20000 [ 11%] (Warmup)
## Chain 1 Iteration: 2300 / 20000 [ 11%] (Warmup)
## Chain 1 Iteration: 2400 / 20000 [ 12%] (Warmup)
## Chain 1 Iteration: 2500 / 20000 [ 12%] (Warmup)
## Chain 1 Iteration: 2600 / 20000 [ 13%] (Warmup)
## Chain 1 Iteration: 2700 / 20000 [ 13%] (Warmup)
## Chain 1 Iteration: 2800 / 20000 [ 14%] (Warmup)
## Chain 1 Iteration: 2900 / 20000 [ 14%] (Warmup)
## Chain 1 Iteration: 3000 / 20000 [ 15%] (Warmup)
## Chain 1 Iteration: 3100 / 20000 [ 15%] (Warmup)
## Chain 1 Iteration: 3200 / 20000 [ 16%] (Warmup)
## Chain 1 Iteration: 3300 / 20000 [ 16%] (Warmup)
## Chain 1 Iteration: 3400 / 20000 [ 17%] (Warmup)
## Chain 1 Iteration: 3500 / 20000 [ 17%] (Warmup)
## Chain 1 Iteration: 3600 / 20000 [ 18%] (Warmup)
## Chain 1 Iteration: 3700 / 20000 [ 18%] (Warmup)
## Chain 1 Iteration: 3800 / 20000 [ 19%] (Warmup)
## Chain 1 Iteration: 3900 / 20000 [ 19%] (Warmup)
## Chain 1 Iteration: 4000 / 20000 [ 20%] (Warmup)
## Chain 1 Iteration: 4100 / 20000 [ 20%] (Warmup)
## Chain 1 Iteration: 4200 / 20000 [ 21%] (Warmup)
## Chain 1 Iteration: 4300 / 20000 [ 21%] (Warmup)
## Chain 1 Iteration: 4400 / 20000 [ 22%] (Warmup)
## Chain 1 Iteration: 4500 / 20000 [ 22%] (Warmup)
## Chain 1 Iteration: 4600 / 20000 [ 23%] (Warmup)
## Chain 1 Iteration: 4700 / 20000 [ 23%] (Warmup)
## Chain 1 Iteration: 4800 / 20000 [ 24%] (Warmup)
## Chain 1 Iteration: 4900 / 20000 [ 24%] (Warmup)
## Chain 1 Iteration: 5000 / 20000 [ 25%] (Warmup)
## Chain 1 Iteration: 5100 / 20000 [ 25%] (Warmup)
## Chain 1 Iteration: 5200 / 20000 [ 26%] (Warmup)
## Chain 1 Iteration: 5300 / 20000 [ 26%] (Warmup)
## Chain 1 Iteration: 5400 / 20000 [ 27%] (Warmup)
## Chain 1 Iteration: 5500 / 20000 [ 27%] (Warmup)
## Chain 1 Iteration: 5600 / 20000 [ 28%] (Warmup)
## Chain 1 Iteration: 5700 / 20000 [ 28%] (Warmup)
## Chain 1 Iteration: 5800 / 20000 [ 29%] (Warmup)
## Chain 1 Iteration: 5900 / 20000 [ 29%] (Warmup)
## Chain 1 Iteration: 6000 / 20000 [ 30%] (Warmup)
## Chain 1 Iteration: 6100 / 20000 [ 30%] (Warmup)
## Chain 1 Iteration: 6200 / 20000 [ 31%] (Warmup)
## Chain 1 Iteration: 6300 / 20000 [ 31%] (Warmup)
## Chain 1 Iteration: 6400 / 20000 [ 32%] (Warmup)
## Chain 1 Iteration: 6500 / 20000 [ 32%] (Warmup)
## Chain 1 Iteration: 6600 / 20000 [ 33%] (Warmup)
## Chain 1 Iteration: 6700 / 20000 [ 33%] (Warmup)
## Chain 1 Iteration: 6800 / 20000 [ 34%] (Warmup)
## Chain 1 Iteration: 6900 / 20000 [ 34%] (Warmup)
## Chain 1 Iteration: 7000 / 20000 [ 35%] (Warmup)
## Chain 1 Iteration: 7100 / 20000 [ 35%] (Warmup)
## Chain 1 Iteration: 7200 / 20000 [ 36%] (Warmup)
## Chain 1 Iteration: 7300 / 20000 [ 36%] (Warmup)
## Chain 1 Iteration: 7400 / 20000 [ 37%] (Warmup)
## Chain 1 Iteration: 7500 / 20000 [ 37%] (Warmup)
## Chain 1 Iteration: 7600 / 20000 [ 38%] (Warmup)
## Chain 1 Iteration: 7700 / 20000 [ 38%] (Warmup)
## Chain 1 Iteration: 7800 / 20000 [ 39%] (Warmup)
## Chain 1 Iteration: 7900 / 20000 [ 39%] (Warmup)
## Chain 1 Iteration: 8000 / 20000 [ 40%] (Warmup)
## Chain 1 Iteration: 8100 / 20000 [ 40%] (Warmup)
## Chain 1 Iteration: 8200 / 20000 [ 41%] (Warmup)
## Chain 1 Iteration: 8300 / 20000 [ 41%] (Warmup)
## Chain 1 Iteration: 8400 / 20000 [ 42%] (Warmup)
## Chain 1 Iteration: 8500 / 20000 [ 42%] (Warmup)
## Chain 1 Iteration: 8600 / 20000 [ 43%] (Warmup)
## Chain 1 Iteration: 8700 / 20000 [ 43%] (Warmup)
## Chain 1 Iteration: 8800 / 20000 [ 44%] (Warmup)
## Chain 1 Iteration: 8900 / 20000 [ 44%] (Warmup)
## Chain 1 Iteration: 9000 / 20000 [ 45%] (Warmup)
## Chain 1 Iteration: 9100 / 20000 [ 45%] (Warmup)
## Chain 1 Iteration: 9200 / 20000 [ 46%] (Warmup)
## Chain 1 Iteration: 9300 / 20000 [ 46%] (Warmup)
## Chain 1 Iteration: 9400 / 20000 [ 47%] (Warmup)
## Chain 1 Iteration: 9500 / 20000 [ 47%] (Warmup)
## Chain 1 Iteration: 9600 / 20000 [ 48%] (Warmup)
## Chain 1 Iteration: 9700 / 20000 [ 48%] (Warmup)
## Chain 1 Iteration: 9800 / 20000 [ 49%] (Warmup)
## Chain 1 Iteration: 9900 / 20000 [ 49%] (Warmup)
## Chain 1 Iteration: 10000 / 20000 [ 50%] (Warmup)
## Chain 1 Iteration: 10001 / 20000 [ 50%] (Sampling)
## Chain 1 Iteration: 10100 / 20000 [ 50%] (Sampling)
## Chain 1 Iteration: 10200 / 20000 [ 51%] (Sampling)
## Chain 1 Iteration: 10300 / 20000 [ 51%] (Sampling)
## Chain 1 Iteration: 10400 / 20000 [ 52%] (Sampling)
## Chain 1 Iteration: 10500 / 20000 [ 52%] (Sampling)
## Chain 1 Iteration: 10600 / 20000 [ 53%] (Sampling)
## Chain 1 Iteration: 10700 / 20000 [ 53%] (Sampling)
## Chain 1 Iteration: 10800 / 20000 [ 54%] (Sampling)
## Chain 1 Iteration: 10900 / 20000 [ 54%] (Sampling)
## Chain 1 Iteration: 11000 / 20000 [ 55%] (Sampling)
## Chain 1 Iteration: 11100 / 20000 [ 55%] (Sampling)
## Chain 1 Iteration: 11200 / 20000 [ 56%] (Sampling)
## Chain 1 Iteration: 11300 / 20000 [ 56%] (Sampling)
## Chain 1 Iteration: 11400 / 20000 [ 57%] (Sampling)
## Chain 1 Iteration: 11500 / 20000 [ 57%] (Sampling)
## Chain 1 Iteration: 11600 / 20000 [ 58%] (Sampling)
## Chain 1 Iteration: 11700 / 20000 [ 58%] (Sampling)
## Chain 1 Iteration: 11800 / 20000 [ 59%] (Sampling)
## Chain 1 Iteration: 11900 / 20000 [ 59%] (Sampling)
## Chain 1 Iteration: 12000 / 20000 [ 60%] (Sampling)
## Chain 1 Iteration: 12100 / 20000 [ 60%] (Sampling)
## Chain 1 Iteration: 12200 / 20000 [ 61%] (Sampling)
## Chain 1 Iteration: 12300 / 20000 [ 61%] (Sampling)
## Chain 1 Iteration: 12400 / 20000 [ 62%] (Sampling)
## Chain 1 Iteration: 12500 / 20000 [ 62%] (Sampling)
## Chain 1 Iteration: 12600 / 20000 [ 63%] (Sampling)
## Chain 1 Iteration: 12700 / 20000 [ 63%] (Sampling)
## Chain 1 Iteration: 12800 / 20000 [ 64%] (Sampling)
## Chain 1 Iteration: 12900 / 20000 [ 64%] (Sampling)
## Chain 1 Iteration: 13000 / 20000 [ 65%] (Sampling)
## Chain 1 Iteration: 13100 / 20000 [ 65%] (Sampling)
## Chain 1 Iteration: 13200 / 20000 [ 66%] (Sampling)
## Chain 1 Iteration: 13300 / 20000 [ 66%] (Sampling)
## Chain 1 Iteration: 13400 / 20000 [ 67%] (Sampling)
## Chain 1 Iteration: 13500 / 20000 [ 67%] (Sampling)
## Chain 1 Iteration: 13600 / 20000 [ 68%] (Sampling)
## Chain 1 Iteration: 13700 / 20000 [ 68%] (Sampling)
## Chain 1 Iteration: 13800 / 20000 [ 69%] (Sampling)
## Chain 1 Iteration: 13900 / 20000 [ 69%] (Sampling)
## Chain 1 Iteration: 14000 / 20000 [ 70%] (Sampling)
## Chain 1 Iteration: 14100 / 20000 [ 70%] (Sampling)
## Chain 1 Iteration: 14200 / 20000 [ 71%] (Sampling)
## Chain 1 Iteration: 14300 / 20000 [ 71%] (Sampling)
## Chain 1 Iteration: 14400 / 20000 [ 72%] (Sampling)
## Chain 1 Iteration: 14500 / 20000 [ 72%] (Sampling)
## Chain 1 Iteration: 14600 / 20000 [ 73%] (Sampling)
## Chain 1 Iteration: 14700 / 20000 [ 73%] (Sampling)
## Chain 1 Iteration: 14800 / 20000 [ 74%] (Sampling)
## Chain 1 Iteration: 14900 / 20000 [ 74%] (Sampling)
## Chain 1 Iteration: 15000 / 20000 [ 75%] (Sampling)
## Chain 1 Iteration: 15100 / 20000 [ 75%] (Sampling)
## Chain 1 Iteration: 15200 / 20000 [ 76%] (Sampling)
## Chain 1 Iteration: 15300 / 20000 [ 76%] (Sampling)
## Chain 1 Iteration: 15400 / 20000 [ 77%] (Sampling)
## Chain 1 Iteration: 15500 / 20000 [ 77%] (Sampling)
## Chain 1 Iteration: 15600 / 20000 [ 78%] (Sampling)
## Chain 1 Iteration: 15700 / 20000 [ 78%] (Sampling)
## Chain 1 Iteration: 15800 / 20000 [ 79%] (Sampling)
## Chain 1 Iteration: 15900 / 20000 [ 79%] (Sampling)
## Chain 1 Iteration: 16000 / 20000 [ 80%] (Sampling)
## Chain 1 Iteration: 16100 / 20000 [ 80%] (Sampling)
## Chain 1 Iteration: 16200 / 20000 [ 81%] (Sampling)
## Chain 1 Iteration: 16300 / 20000 [ 81%] (Sampling)
## Chain 1 Iteration: 16400 / 20000 [ 82%] (Sampling)
## Chain 1 Iteration: 16500 / 20000 [ 82%] (Sampling)
## Chain 1 Iteration: 16600 / 20000 [ 83%] (Sampling)
## Chain 1 Iteration: 16700 / 20000 [ 83%] (Sampling)
## Chain 1 Iteration: 16800 / 20000 [ 84%] (Sampling)
## Chain 1 Iteration: 16900 / 20000 [ 84%] (Sampling)
## Chain 1 Iteration: 17000 / 20000 [ 85%] (Sampling)
## Chain 1 Iteration: 17100 / 20000 [ 85%] (Sampling)
## Chain 1 Iteration: 17200 / 20000 [ 86%] (Sampling)
## Chain 1 Iteration: 17300 / 20000 [ 86%] (Sampling)
## Chain 1 Iteration: 17400 / 20000 [ 87%] (Sampling)
## Chain 1 Iteration: 17500 / 20000 [ 87%] (Sampling)
## Chain 1 Iteration: 17600 / 20000 [ 88%] (Sampling)
## Chain 1 Iteration: 17700 / 20000 [ 88%] (Sampling)
## Chain 1 Iteration: 17800 / 20000 [ 89%] (Sampling)
## Chain 1 Iteration: 17900 / 20000 [ 89%] (Sampling)
## Chain 1 Iteration: 18000 / 20000 [ 90%] (Sampling)
## Chain 1 Iteration: 18100 / 20000 [ 90%] (Sampling)
## Chain 1 Iteration: 18200 / 20000 [ 91%] (Sampling)
## Chain 1 Iteration: 18300 / 20000 [ 91%] (Sampling)
## Chain 1 Iteration: 18400 / 20000 [ 92%] (Sampling)
## Chain 1 Iteration: 18500 / 20000 [ 92%] (Sampling)
## Chain 1 Iteration: 18600 / 20000 [ 93%] (Sampling)
## Chain 1 Iteration: 18700 / 20000 [ 93%] (Sampling)
## Chain 1 Iteration: 18800 / 20000 [ 94%] (Sampling)
## Chain 1 Iteration: 18900 / 20000 [ 94%] (Sampling)
## Chain 1 Iteration: 19000 / 20000 [ 95%] (Sampling)
## Chain 1 Iteration: 19100 / 20000 [ 95%] (Sampling)
## Chain 1 Iteration: 19200 / 20000 [ 96%] (Sampling)
## Chain 1 Iteration: 19300 / 20000 [ 96%] (Sampling)
## Chain 1 Iteration: 19400 / 20000 [ 97%] (Sampling)
## Chain 1 Iteration: 19500 / 20000 [ 97%] (Sampling)
## Chain 1 Iteration: 19600 / 20000 [ 98%] (Sampling)
## Chain 1 Iteration: 19700 / 20000 [ 98%] (Sampling)
## Chain 1 Iteration: 19800 / 20000 [ 99%] (Sampling)
## Chain 1 Iteration: 19900 / 20000 [ 99%] (Sampling)
## Chain 1 Iteration: 20000 / 20000 [100%] (Sampling)
## Chain 1 finished in 0.2 seconds.
# prior for females
pF <- inv_logit( prior$a[,1])
dens(pF, adj=0.1, xlab="Prior Female Admission Rates")
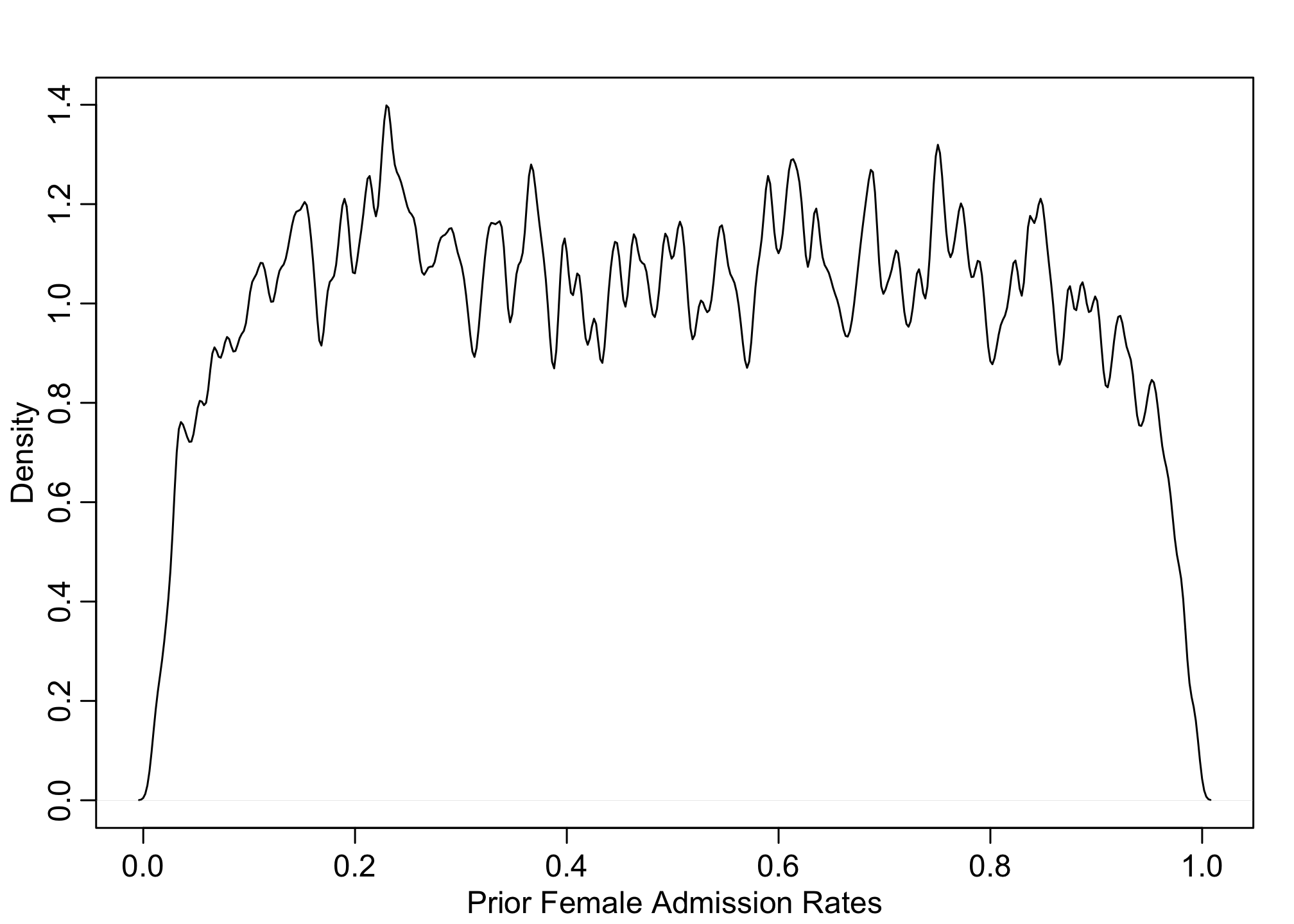
# prior for males
pM <- inv_logit( prior$a[,2])
dens(pM, adj=0.1, xlab="Prior Male Admission Rates")
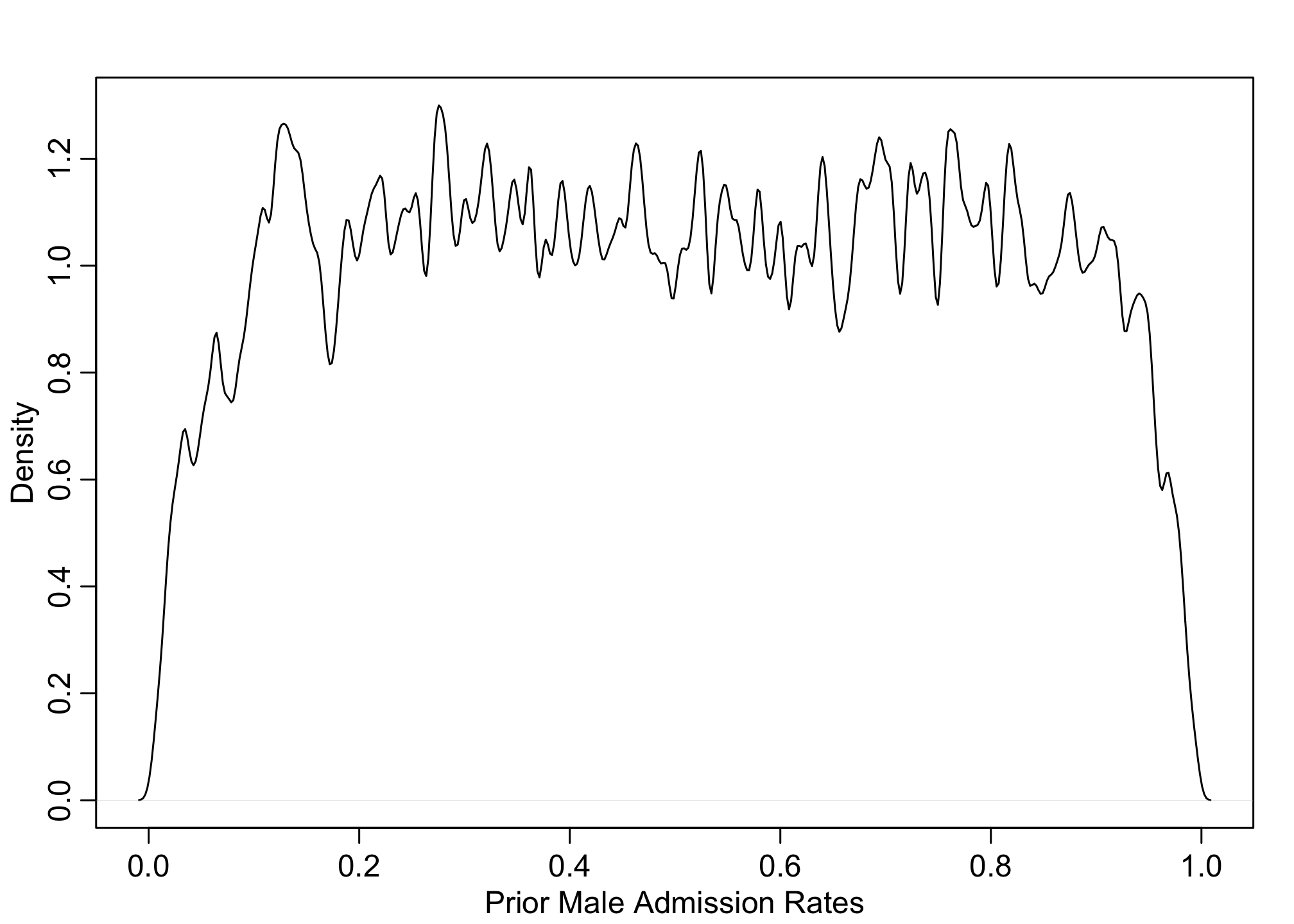
These posteriors makes sense as we’d expect the application rates to be somewhere between 0.1 - 0.9. But this is only the probability for Females and Males individually (let alone they’re identical), but not their contrasts. We can also calculate priors for the gender causal effect.
dens(abs( pF - pM), adj = 0.1)
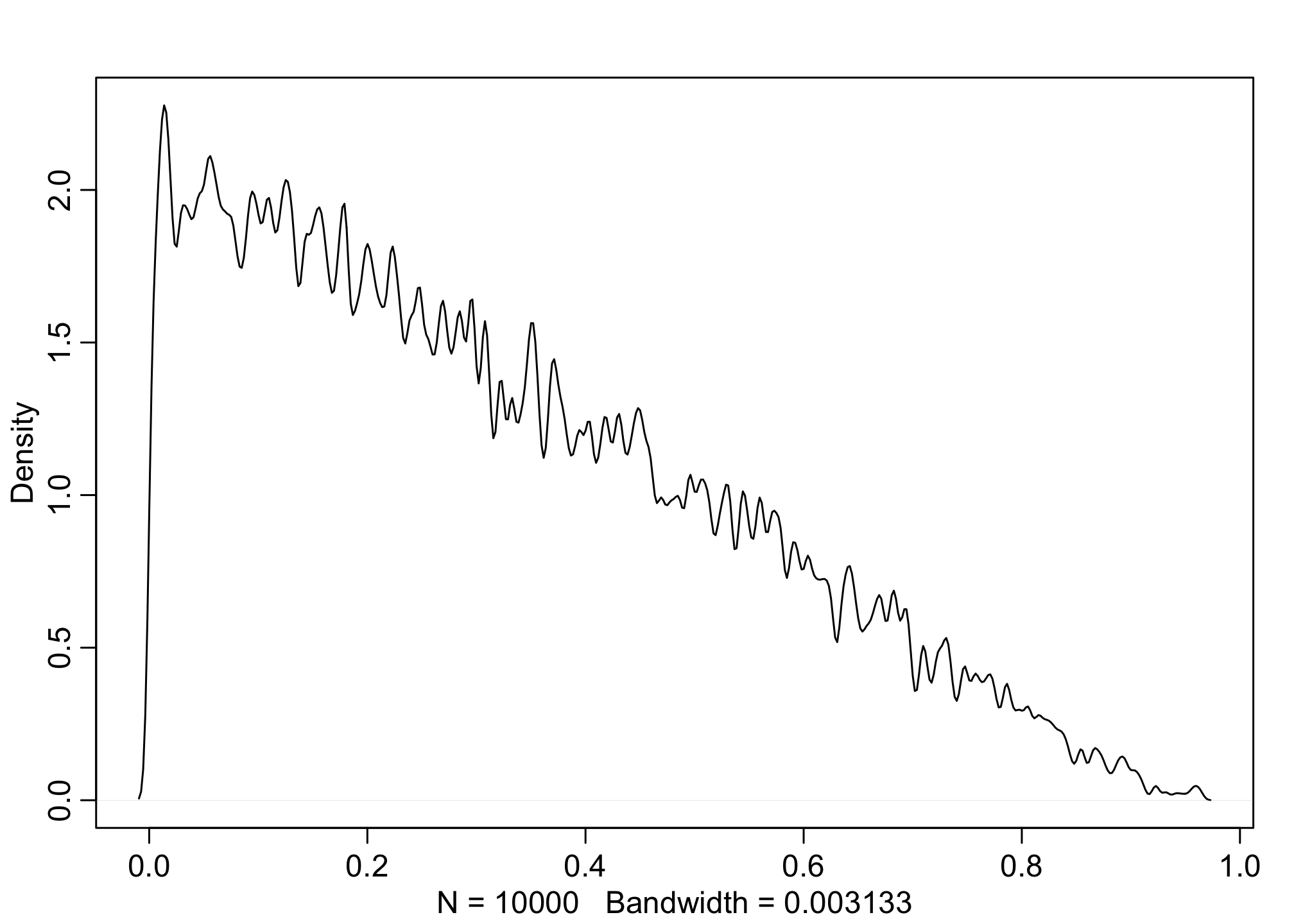
These are what we’d expect. If you’re not sure why, make sure to go through section 11.1 in the book where Richard discusses implications for the prior in Binomial regressions, especially where too wide of prior sigma’s can have a bad effect on the priors. Alternatively, change the model above to a wider prior for the alpha and see what happens.
Analyze the Model
m11.7 <- ulam(
alist(
A ~ dbinom( N , p ) ,
logit(p) <- a[G] ,
a[G] ~ dnorm( 0 , 1.5 )
) , data = dat_list, chains = 4
)
## Running MCMC with 4 sequential chains, with 1 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 1 finished in 0.0 seconds.
## Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 2 finished in 0.0 seconds.
## Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 3 finished in 0.0 seconds.
## Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 4 finished in 0.0 seconds.
##
## All 4 chains finished successfully.
## Mean chain execution time: 0.0 seconds.
## Total execution time: 0.7 seconds.
precis( m11.7, depth = 2)
## mean sd 5.5% 94.5% n_eff Rhat4
## a[1] -0.2201691 0.03962597 -0.2837434 -0.1574992 1452.163 1.000439
## a[2] -0.8304064 0.04954410 -0.9103124 -0.7540644 1459.525 1.002937
The posterior for males a[1] is higher than that of female applications. We’ll need to calculate the contrasts to much how much higher.
But before that, let’s also consider convergence criteria.
Convergence Diagnostics
First, we can see that both coefficients Rhat values are near to 1, which is what we would like.
We can also run trace and trank plots:
traceplot(m11.7)
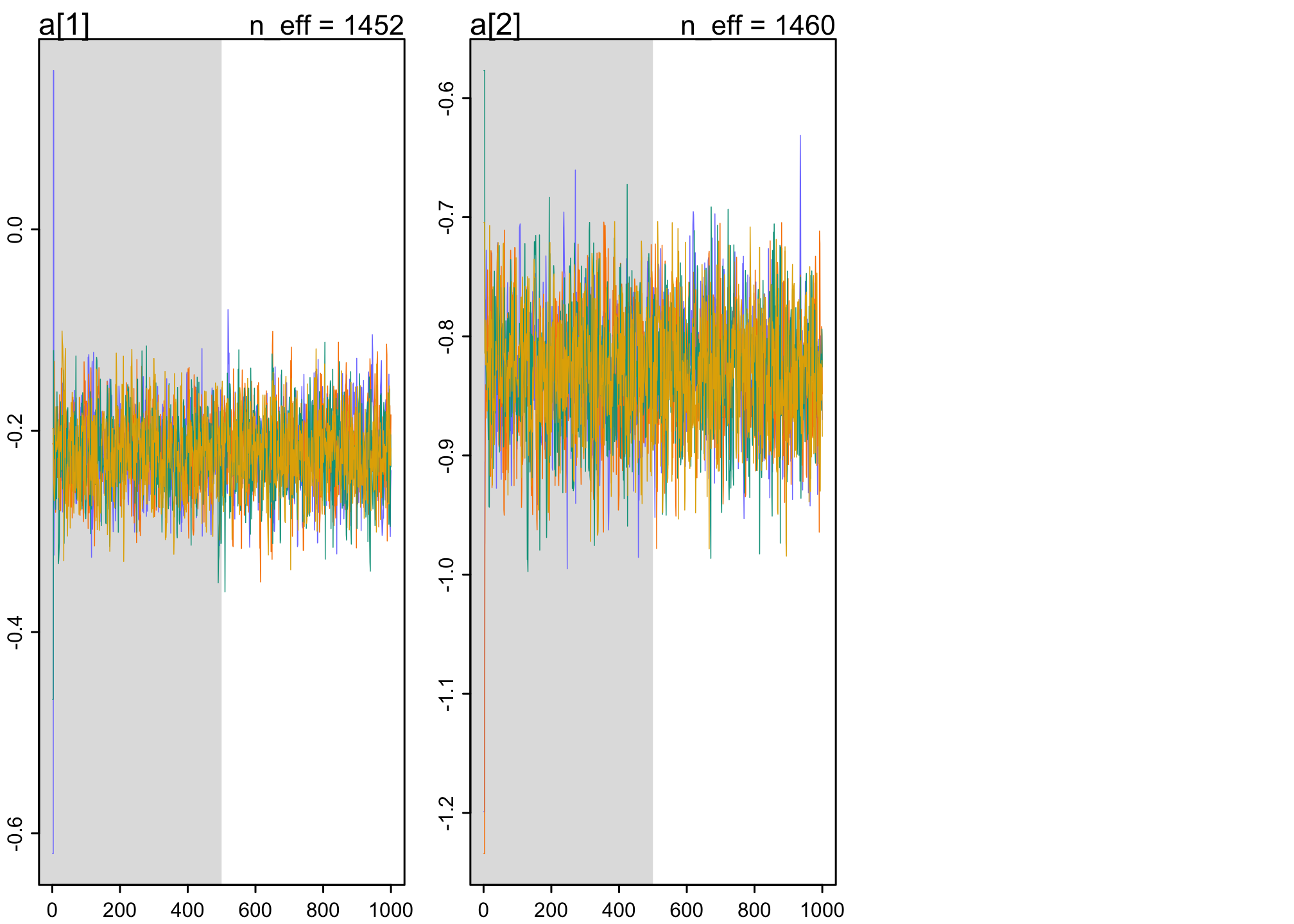
trankplot(m11.7)
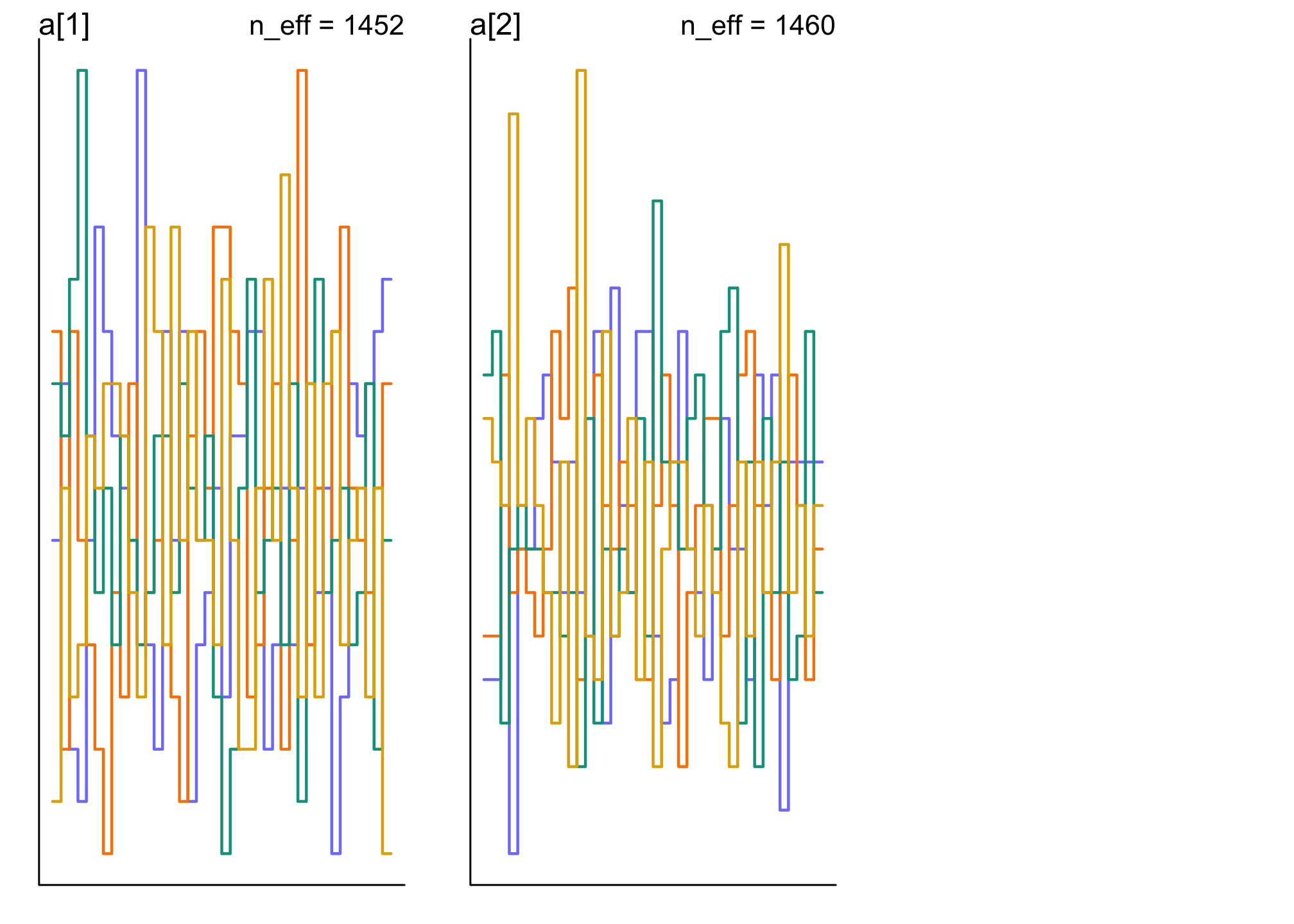
These are good. The traceplots are like “hairy caterpillars” and the trankplots show “mixture” so that no one chain is higher/lower than others.
Prediction
Now let’s calculate the contrasts.
post <- extract.samples(m11.7)
diff_a <- post$a[,1] - post$a[,2]
diff_p <- inv_logit(post$a[,1]) - inv_logit(post$a[,2])
precis( list( diff_a=diff_a , diff_p=diff_p))
## mean sd 5.5% 94.5% histogram
## diff_a 0.6102373 0.06380121 0.5092443 0.7137152 ▁▁▃▇▇▅▂▁
## diff_p 0.1415393 0.01441388 0.1189685 0.1653068 ▁▁▁▅▇▇▅▂▁▁
dens( diff_p, lwd=4, col=2, xlab="F-M contrast (total)")
abline( v=0, lty=3)
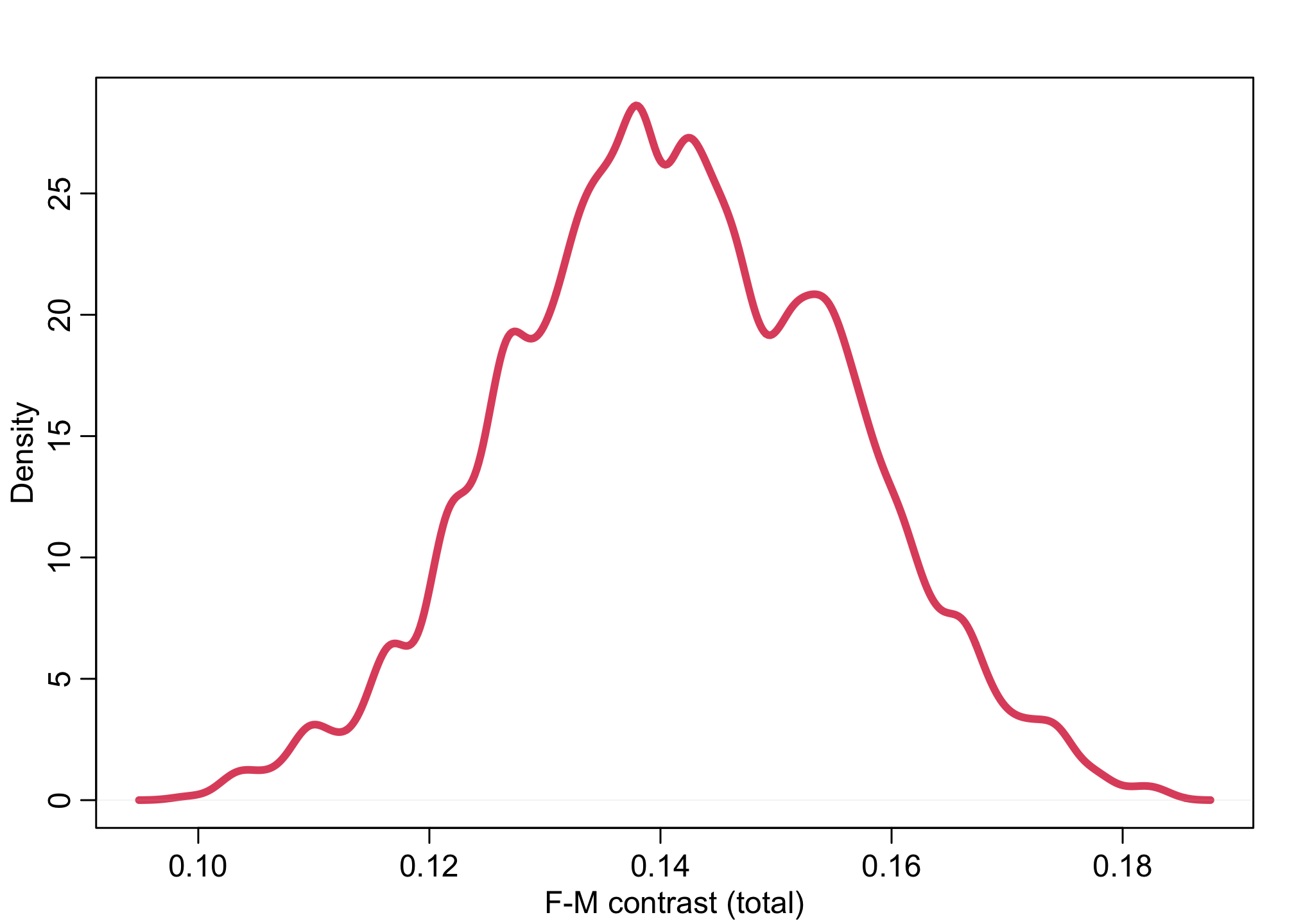
On the probability scale (diff_p), the difference is about a 12-16% percent higher admission rate for males than females.
But let’s now also do a posterior predictive (validation) check on each of the 18 individuals.
Posterior predictive check
postcheck(m11.7)
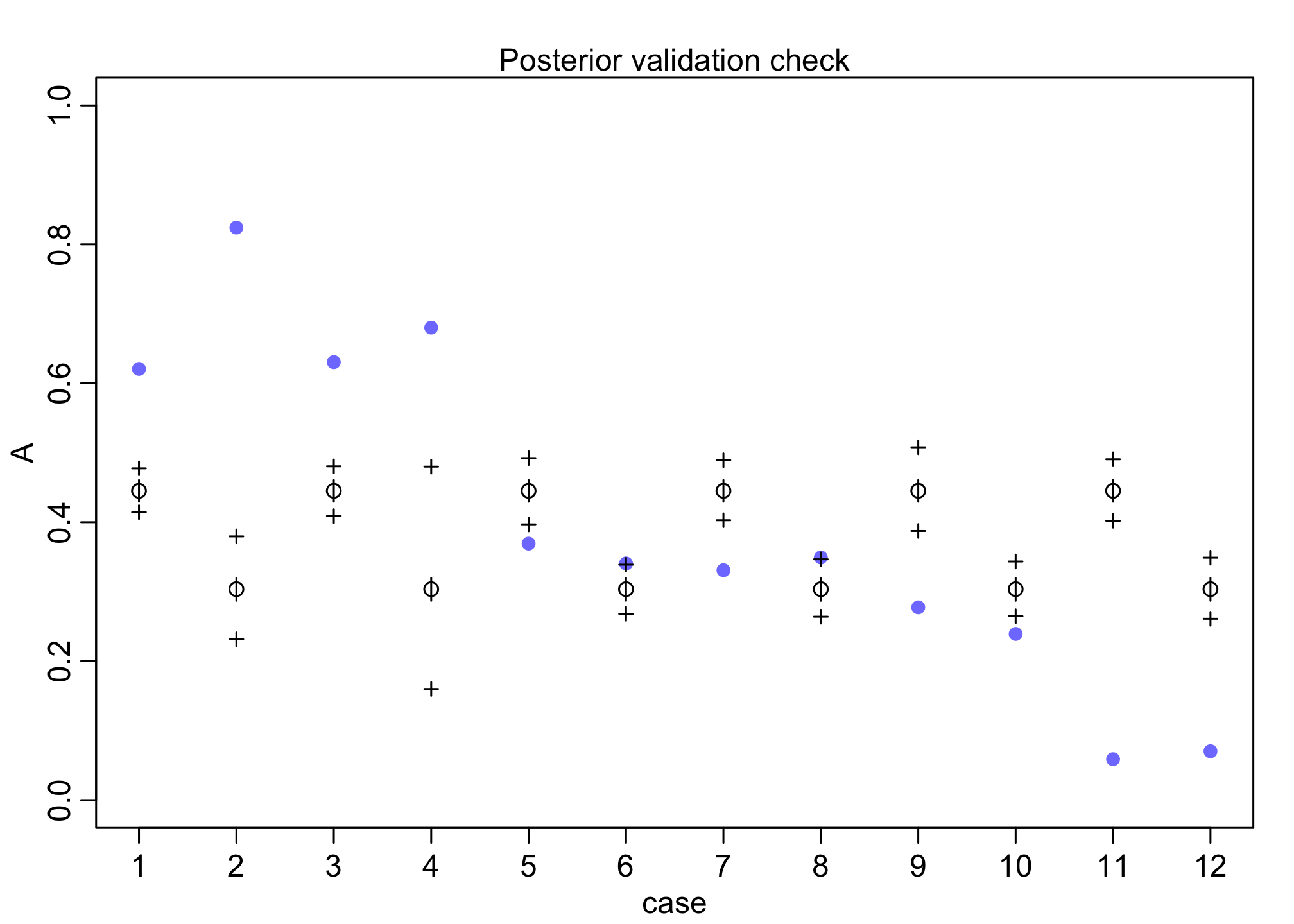
As discussed on page 342, these predictions aren’t great (e.g., cases 1-4 and 11-12). As mentioned, the model did correctly answer: “What are the average probabilities of admissions for women and men, across all departments?”
The problem is students self-select application by gender, namely women have different application rates by department. More difficult, women tend to apply more to most selective departments which drives more of the lower rate of admissions on total effect than the direct effect.
However, what we’re really interested in is: “What is the average difference in probability of admission between women and men within departments?” That is conditioning on department (aka direct effect)
If this doesn’t make sense, watch Richard’s lecture 12 from his Fall 2019 class.
This was also considered on pages 343-345 and you may need this for problem set 6.
Package versions
sessionInfo()
## R version 4.1.1 (2021-08-10)
## Platform: aarch64-apple-darwin20 (64-bit)
## Running under: macOS Monterey 12.1
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRlapack.dylib
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## attached base packages:
## [1] parallel stats graphics grDevices datasets utils methods
## [8] base
##
## other attached packages:
## [1] digest_0.6.29 dagitty_0.3-1 rethinking_2.21
## [4] cmdstanr_0.4.0.9001 rstan_2.21.3 ggplot2_3.3.5
## [7] StanHeaders_2.21.0-7
##
## loaded via a namespace (and not attached):
## [1] sass_0.4.0 jsonlite_1.7.2 bslib_0.3.1
## [4] RcppParallel_5.1.4 assertthat_0.2.1 posterior_1.1.0
## [7] distributional_0.2.2 highr_0.9 stats4_4.1.1
## [10] tensorA_0.36.2 renv_0.14.0 yaml_2.2.1
## [13] pillar_1.6.4 backports_1.4.1 lattice_0.20-44
## [16] glue_1.6.0 checkmate_2.0.0 colorspace_2.0-2
## [19] htmltools_0.5.2 pkgconfig_2.0.3 bookdown_0.24
## [22] purrr_0.3.4 mvtnorm_1.1-3 scales_1.1.1
## [25] processx_3.5.2 tibble_3.1.6 generics_0.1.1
## [28] farver_2.1.0 ellipsis_0.3.2 withr_2.4.3
## [31] cli_3.1.0 magrittr_2.0.1 crayon_1.4.2
## [34] mime_0.12 evaluate_0.14 ps_1.6.0
## [37] fs_1.5.0 fansi_0.5.0 MASS_7.3-54
## [40] pkgbuild_1.3.1 blogdown_1.5 data.table_1.14.2
## [43] tools_4.1.1 loo_2.4.1 prettyunits_1.1.1
## [46] lifecycle_1.0.1 matrixStats_0.61.0 stringr_1.4.0
## [49] V8_3.6.0 munsell_0.5.0 callr_3.7.0
## [52] compiler_4.1.1 jquerylib_0.1.4 rlang_0.4.12
## [55] grid_4.1.1 rstudioapi_0.13 base64enc_0.1-3
## [58] rmarkdown_2.11 boot_1.3-28 gtable_0.3.0
## [61] codetools_0.2-18 curl_4.3.2 inline_0.3.19
## [64] abind_1.4-5 DBI_1.1.1 R6_2.5.1
## [67] gridExtra_2.3 lubridate_1.8.0 knitr_1.36
## [70] dplyr_1.0.7 fastmap_1.1.0 utf8_1.2.2
## [73] downloadthis_0.2.1 bsplus_0.1.3 shape_1.4.6
## [76] stringi_1.7.6 Rcpp_1.0.7 vctrs_0.3.8
## [79] tidyselect_1.1.1 xfun_0.28 coda_0.19-4