Problem Set 6 Solutions
This problem set is optional and not necessary to be submitted. We will try to work on it in class on March 14.
Question 1
The data in data(NWOGrants) are outcomes for scientific funding applications for the Netherlands Organization for Scientific Research (NWO) from 2010-2012. These data have a very similar structure to the UCBAdmit data discussed in Chapter 11. Draw a DAG for this sample and then use one or more binomial GLMs to estimate the TOTAL causal effect of gender on grant awards.
library(rethinking)
data(NWOGrants)
d <- NWOGrants
head(d)
## discipline gender applications awards
## 1 Chemical sciences m 83 22
## 2 Chemical sciences f 39 10
## 3 Physical sciences m 135 26
## 4 Physical sciences f 39 9
## 5 Physics m 67 18
## 6 Physics f 9 2
Let’s plot the DAG.
library(dagitty)
g <- dagitty('dag {
bb="0,0,1,1"
G [pos="0.251,0.481"]
D [pos="0.251,0.352"]
A [pos="0.481,0.352"]
G -> D
G -> A
D -> A
}
')
plot(g)

Since Department is a mediator, we would not condition by it to find the total causal effect of gender on awards.
dat <- list(
A = as.integer(d$awards),
N = as.integer(d$applications),
G = ifelse( d$gender=="m" , 1L , 2L ) ,
D = as.integer(d$discipline)
)
m1 <- ulam(
alist(
A ~ dbinom( N, p ) ,
logit(p) <- a[G] ,
a[G] ~ dnorm(0, 1.5)
) , data = dat, chains = 4
)
## Running MCMC with 4 sequential chains, with 1 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 1 finished in 0.0 seconds.
## Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 2 finished in 0.0 seconds.
## Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 3 finished in 0.0 seconds.
## Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 4 finished in 0.0 seconds.
##
## All 4 chains finished successfully.
## Mean chain execution time: 0.0 seconds.
## Total execution time: 0.7 seconds.
precis(m1, depth = 2)
## mean sd 5.5% 94.5% n_eff Rhat4
## a[1] -1.529911 0.06482889 -1.631014 -1.424725 1374.110 1.002098
## a[2] -1.740197 0.08196258 -1.870830 -1.613570 1447.698 0.999101
Before looking at the contrasts (causal effect), we’ll look at convergence statistics. The Rhat’s are 1 which are good. Let’s also look at the trace and trank plots.
traceplot(m1)
trankplot(m1)
Therefore, our model has appropriate convergence statistics.
We’ll need to calculate the contrasts to make a determination of the total causal effect of gender on awards.
post1 <- extract.samples(m1)
post1$pGf <- inv_logit(post1$a[,1])
post1$pGm <- inv_logit(post1$a[,2])
post1$G_contrast <- post1$pGf - post1$pGm
dens( post1$G_contrast, lwd=4, col=2, xlab="F-M contrast (total)")
abline( v=0, lty=3)
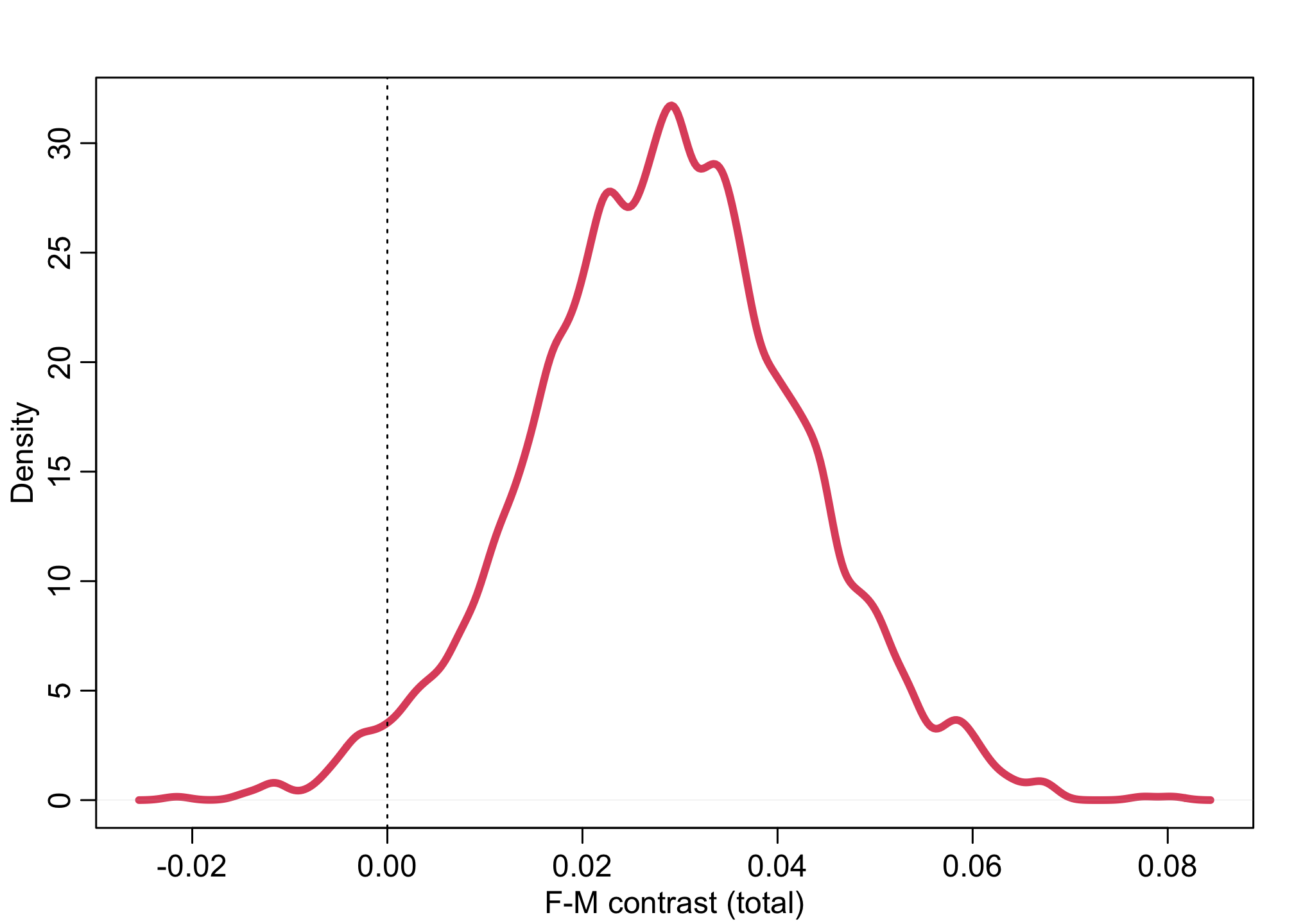
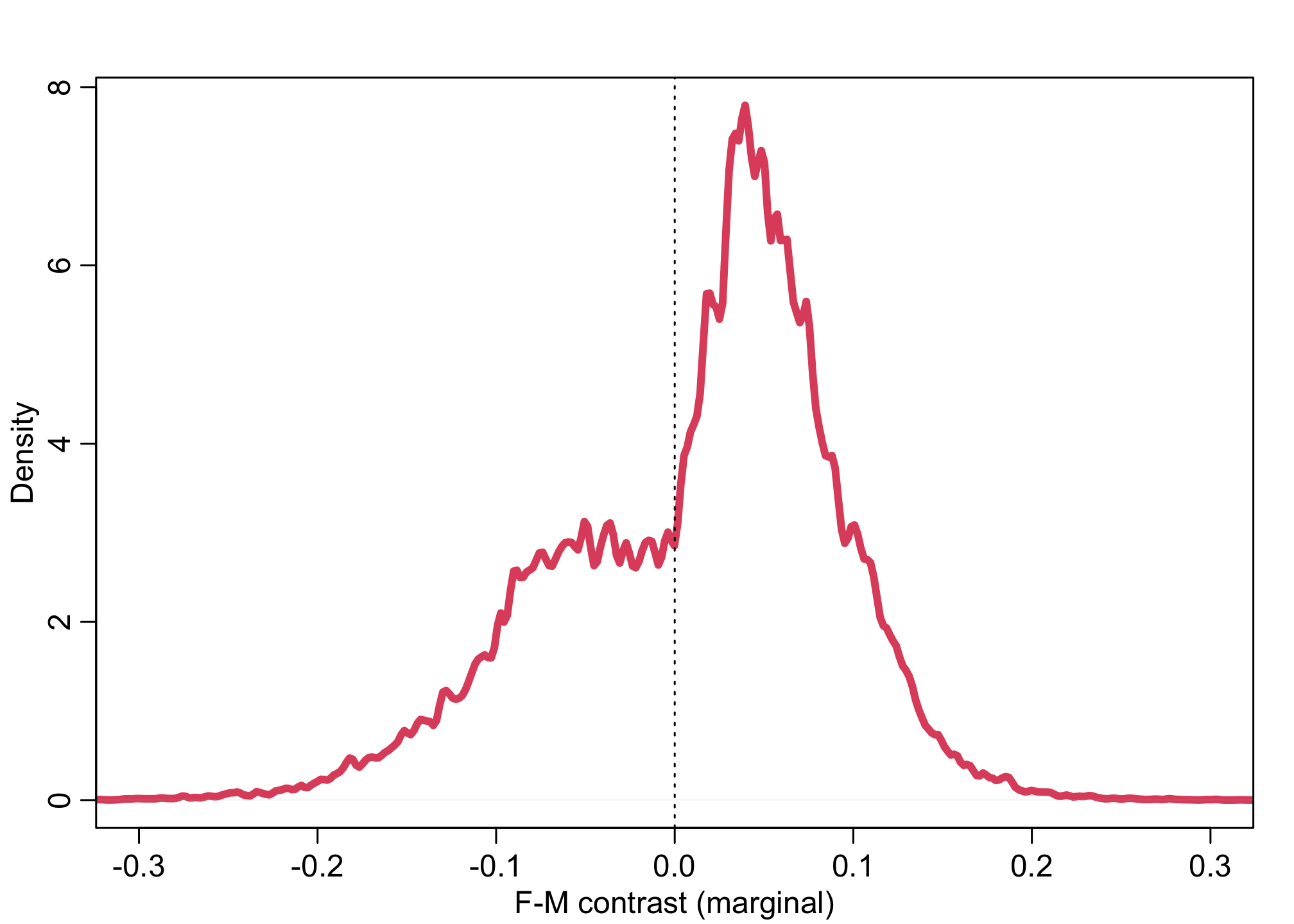
We find about a 3% difference on average for men over women. This could be significant.
We can also do a posterior predictive (validation) check on each of the 18 individuals.
postcheck(m1)
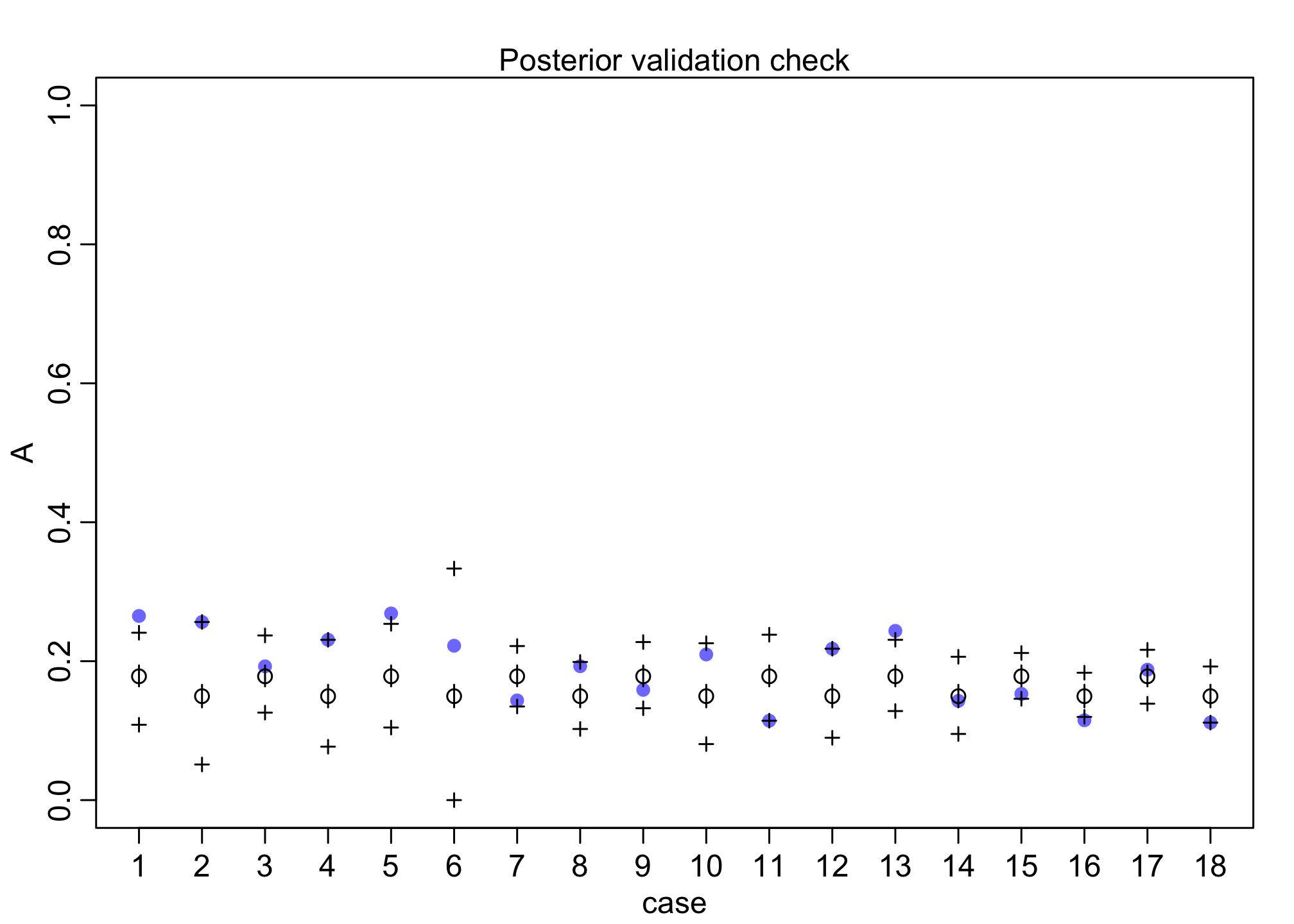
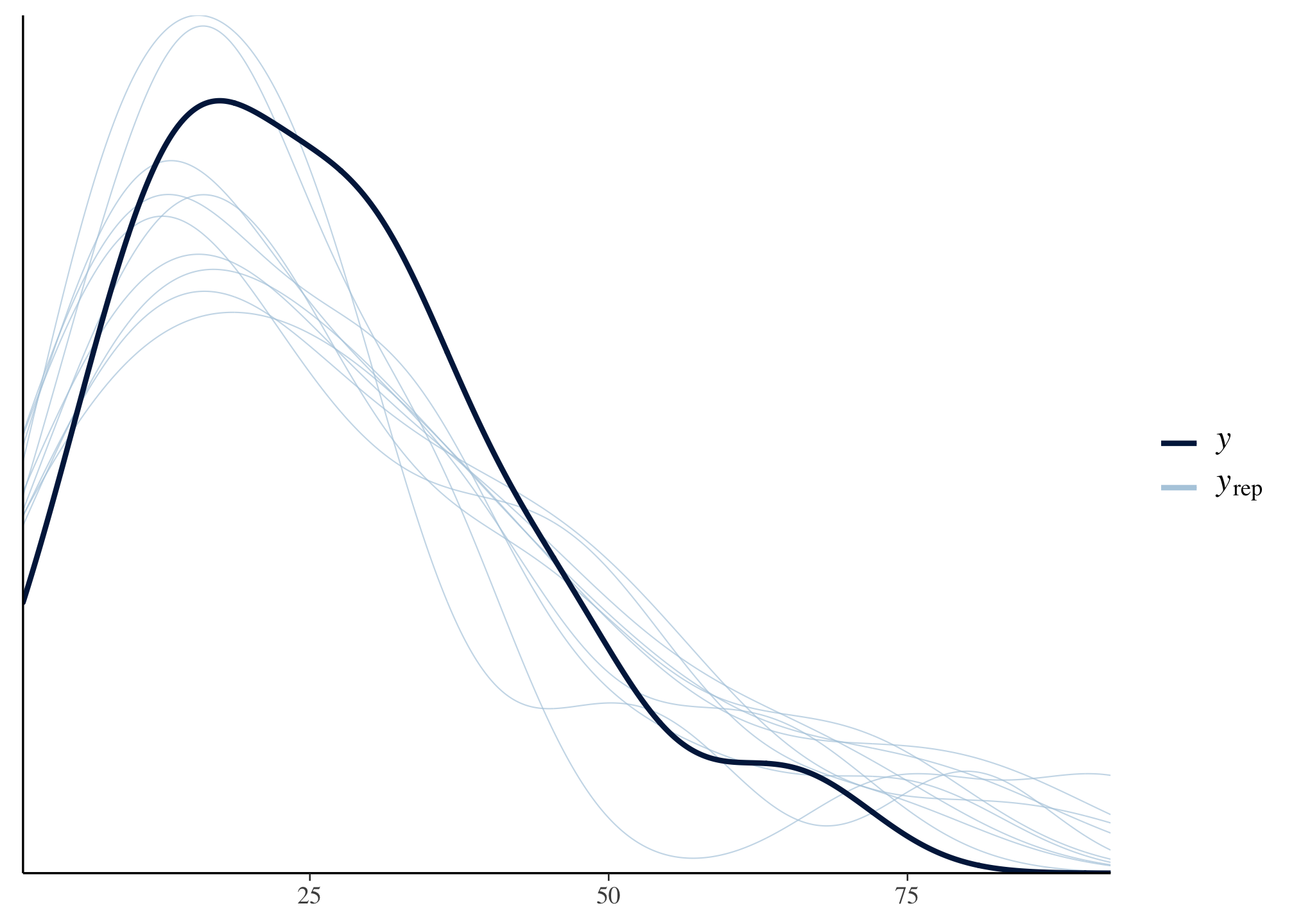
For each individual, the model fits okay but not great.
Alternative approach
You may also use the brms package for this model along with tidyverse based packages.
library(brms)
m1_brms <- brm(awards | trials(applications) ~ gender, family = binomial("logit"), prior = set_prior("normal(0,1.5)", class = "b"), data = d, chains = 4)
##
## SAMPLING FOR MODEL '07311d06eaed335b1371c9568f20ecc2' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 9.2e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.92 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 0.015024 seconds (Warm-up)
## Chain 1: 0.016784 seconds (Sampling)
## Chain 1: 0.031808 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL '07311d06eaed335b1371c9568f20ecc2' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 5e-06 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 0.015295 seconds (Warm-up)
## Chain 2: 0.014512 seconds (Sampling)
## Chain 2: 0.029807 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL '07311d06eaed335b1371c9568f20ecc2' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 4e-06 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 0.015559 seconds (Warm-up)
## Chain 3: 0.013756 seconds (Sampling)
## Chain 3: 0.029315 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL '07311d06eaed335b1371c9568f20ecc2' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 5e-06 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 0.014645 seconds (Warm-up)
## Chain 4: 0.014611 seconds (Sampling)
## Chain 4: 0.029256 seconds (Total)
## Chain 4:
summary(m1_brms)
## Family: binomial
## Links: mu = logit
## Formula: awards | trials(applications) ~ gender
## Data: d (Number of observations: 18)
## Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup draws = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept -1.74 0.08 -1.91 -1.59 1.00 2270 2386
## genderm 0.21 0.11 0.01 0.41 1.00 2871 2411
##
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
library(tidybayes)
library(magrittr) # for %>%
library(dplyr)
posterior_draws <- m1_brms %>%
spread_draws(b_genderm,b_Intercept) %>% # sample/draw posteriors
mutate(b_M = b_Intercept + b_genderm) %>% # due to dummy variables
mutate(Contrast = inv_logit(b_Intercept) - inv_logit(b_M))
ggplot(posterior_draws, aes(x = Contrast)) +
geom_density() +
labs(x = "F-M contrast (total)")
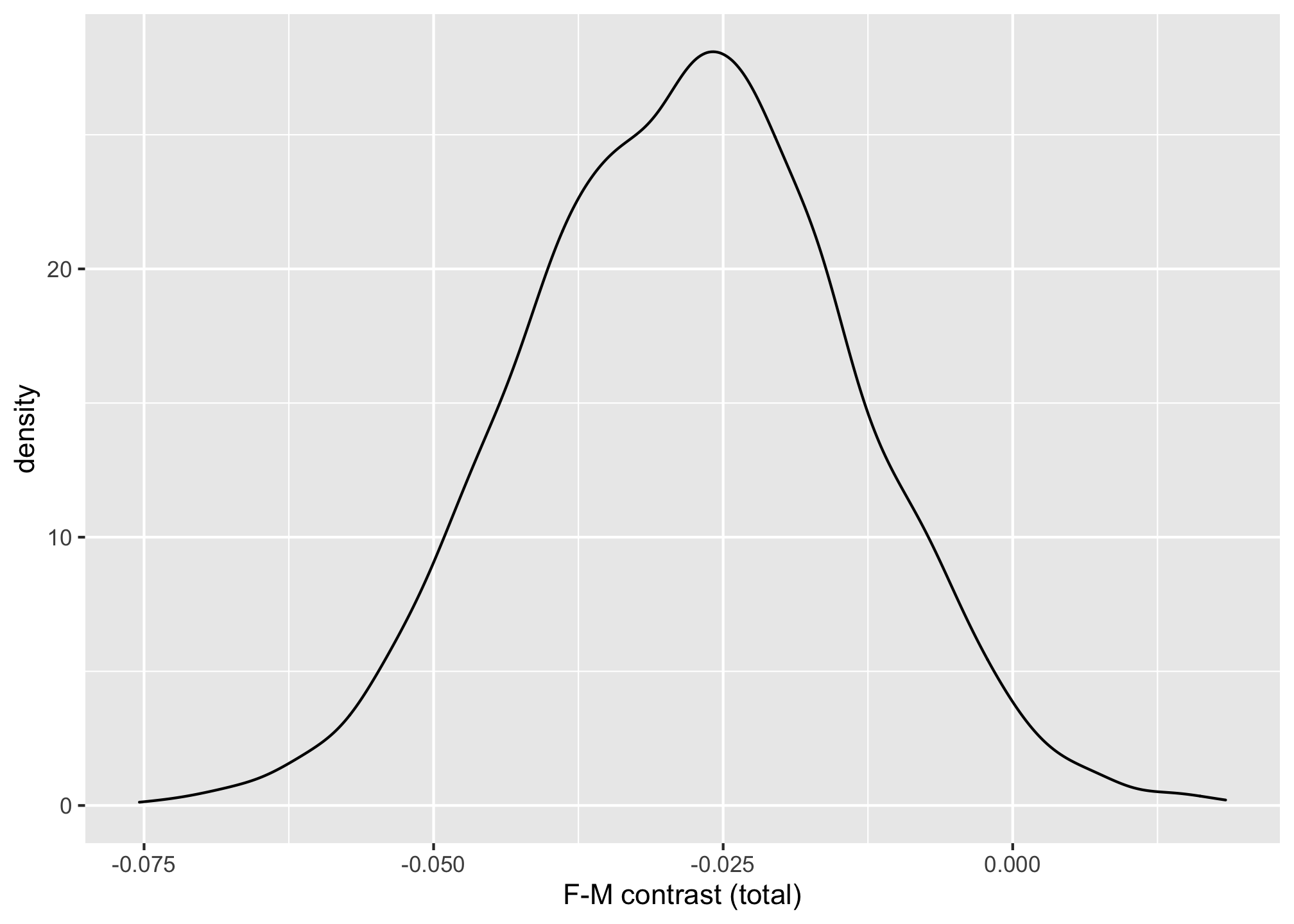
We can check that the posterior contrasts from both approaches are similar.
mean(post1$G_contrast)
## [1] 0.02861795
mean(posterior_draws$Contrast)
## [1] -0.02819377
One nice thing about using brms is there are many other helpful packages. For example, we can easily calculate posterior predictive checks:
bayesplot::pp_check(m1_brms)
Question 2
Now estimate the DIRECT causal effect of gender on grant awards. Compare the average direct causal effect of gender, weighting each discipline in proportion to the number of applications in the sample. Refer to the marginal effect example in Lecture 9 for help.
m2 <- ulam(
alist(
A ~ dbinom( N, p ) ,
logit(p) <- a[G,D],
matrix[G,D]:a ~ normal(0, 1.5)
) , data = dat, chains = 4
)
## Running MCMC with 4 sequential chains, with 1 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 1 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 1 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 1 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 1 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 1 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 1 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 1 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 1 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 1 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 1 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 1 finished in 0.0 seconds.
## Chain 2 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 2 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 2 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 2 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 2 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 2 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 2 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 2 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 2 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 2 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 2 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 2 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 2 finished in 0.0 seconds.
## Chain 3 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 3 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 3 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 3 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 3 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 3 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 3 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 3 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 3 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 3 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 3 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 3 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 3 finished in 0.0 seconds.
## Chain 4 Iteration: 1 / 1000 [ 0%] (Warmup)
## Chain 4 Iteration: 100 / 1000 [ 10%] (Warmup)
## Chain 4 Iteration: 200 / 1000 [ 20%] (Warmup)
## Chain 4 Iteration: 300 / 1000 [ 30%] (Warmup)
## Chain 4 Iteration: 400 / 1000 [ 40%] (Warmup)
## Chain 4 Iteration: 500 / 1000 [ 50%] (Warmup)
## Chain 4 Iteration: 501 / 1000 [ 50%] (Sampling)
## Chain 4 Iteration: 600 / 1000 [ 60%] (Sampling)
## Chain 4 Iteration: 700 / 1000 [ 70%] (Sampling)
## Chain 4 Iteration: 800 / 1000 [ 80%] (Sampling)
## Chain 4 Iteration: 900 / 1000 [ 90%] (Sampling)
## Chain 4 Iteration: 1000 / 1000 [100%] (Sampling)
## Chain 4 finished in 0.0 seconds.
##
## All 4 chains finished successfully.
## Mean chain execution time: 0.0 seconds.
## Total execution time: 0.7 seconds.
# fyi: an identical way to specify priors in ulam
# we use above as easier for post-modeling calculations
# logit(p) <- a[G] + delta[D] ,
# a[G] ~ dnorm(0, 1.5) ,
# delta[D] ~ dnorm(0, 1.5)
precis(m2, depth = 2)
## [1] mean sd 5.5% 94.5% n_eff Rhat4
## <0 rows> (or 0-length row.names)
Let’s calculate the contrast for gender.
total_apps <- sum(dat$N)
apps_per_disc <- sapply( 1:9 , function(i) sum(dat$N[dat$D==i]) )
pG1 <- link(m2,data=list(
D=rep(1:9,times=apps_per_disc),
N=rep(1,total_apps),
G=rep(1,total_apps)))
pG2 <- link(m2,data=list(
D=rep(1:9,times=apps_per_disc),
N=rep(1,total_apps),
G=rep(2,total_apps)))
dens( pG1 - pG2 , lwd=4 , col=2 , xlab="F-M contrast (marginal)" , xlim=c(-0.3,0.3) )
abline( v=0 , lty=3 )
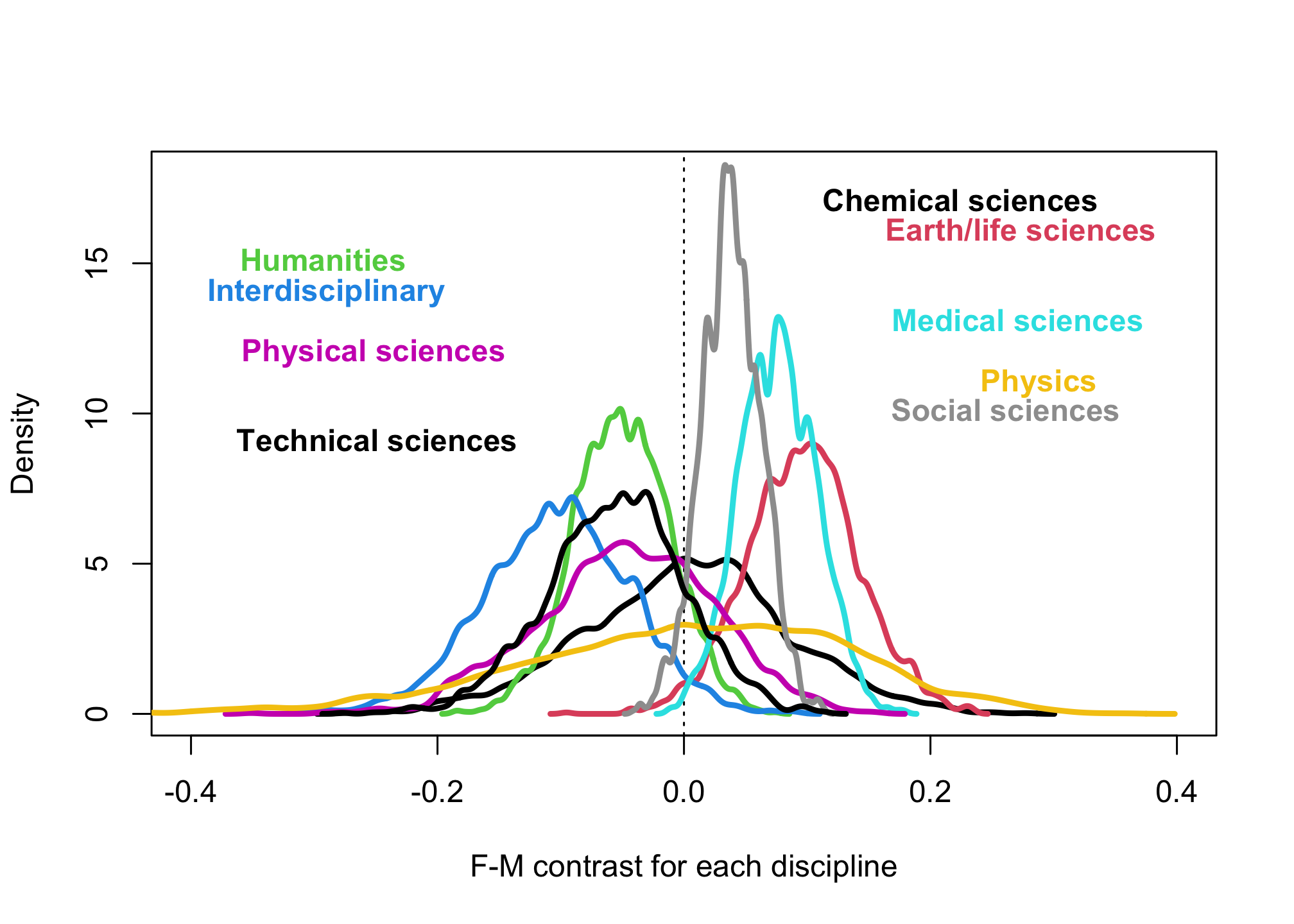
plot( NULL , xlim=c(-0.4,0.4) , ylim=c(0,18) , xlab="F-M contrast for each discipline" , ylab="Density" )
abline( v=0 , lty=3 )
dat$disc <- as.character(d$discipline)
disc <- dat$disc[order(dat$D)]
for ( i in 1:9 ) {
pG1Di <- link(m2,data=list(D=i,N=1,G=1))
pG2Di <- link(m2,data=list(D=i,N=1,G=2))
Gcont <- pG1Di - pG2Di
dens( Gcont , add=TRUE , lwd=3 , col=i )
xloc <- ifelse( mean(Gcont) < 0 , -0.35 , 0.35 )
xpos <- ifelse( mean(Gcont) < 0 , 4 , 2 )
text( xloc + 0.5*mean(Gcont) , 18-i , disc[2*i] , col=i , pos=xpos , font=2 )
}
Question 3
Considering the total effect (problem 1) and direct effect (problem 2) of gender, what causes contribute to the average difference between women and men in award rate in this sample? It is not necessary to say whether or not there is evidence of discrimination. Simply explain how the direct effects you have estimated make sense (or not) of the total effect.
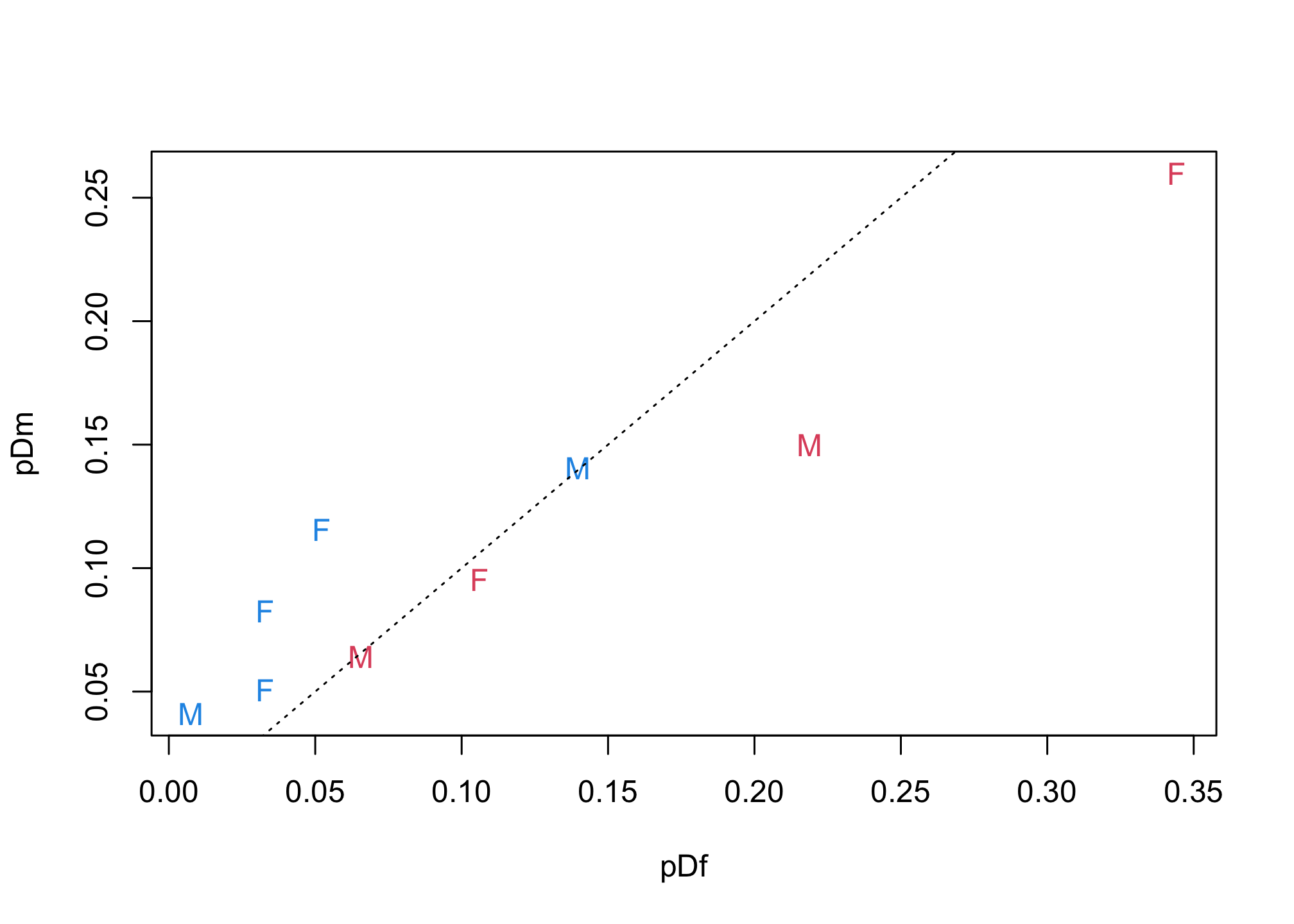
total_f <- sum(d$applications[d$gender=="f"])
pDf <- d$applications[d$gender=="f"] / total_f
total_m <- sum(d$applications[d$gender=="m"])
pDm <- d$applications[d$gender=="m"] / total_m
# overall award rate in each discipline
n_apps <- xtabs( dat$N ~ dat$D )
n_awards <- xtabs( dat$A ~ dat$D )
p_award <- n_awards / n_apps
# f/m award rate in each discipline
post2 <- extract.samples(m2)
pF <- apply( inv_logit(post2$a[,1,]) , 2 , mean )
pM <- apply( inv_logit(post2$a[,2,]) , 2 , mean )
plot( pDf , pDm , lwd=3 , col=ifelse(pDf>pDm,2,4) , pch=ifelse(pF>pM,"F","M") )
abline(a=0,b=1, lty=3)
identify( pDf , pDm , round(p_award,2) )
## integer(0)