Problem Set 4

This problem set is due on February 28, 2022 at 11:59am.

Step 1: Download this file locally.

Step 2: Complete the assignment

Step 3: Knit the assignment as either an html or pdf file.

Step 4: Submit your file here through this canvas link.

• Name:
• UNCC ID:
• Other student worked with (optional):

Question 1

The first two problems are based on the same data. The data in data(foxes) are 116 foxes from 30 different urban groups in England.

library(rethinking)
data(foxes)
d<- foxes
head(d)

##   group avgfood groupsize area weight
## 1     1    0.37         2 1.09   5.02
## 2     1    0.37         2 1.09   2.84
## 3     2    0.53         2 2.05   5.33
## 4     2    0.53         2 2.05   6.07
## 5     3    0.49         2 2.12   5.85
## 6     3    0.49         2 2.12   3.25

These fox groups are like street gangs. Group size (groupsize) varies from 2 to 8 individuals. Each group maintains its own (almost exclusive) urban territory. Some territories are larger than others. The area variable encodes this information. Some territories also have more avgfood than others. And food influences the weight of each fox. Assume this DAG:

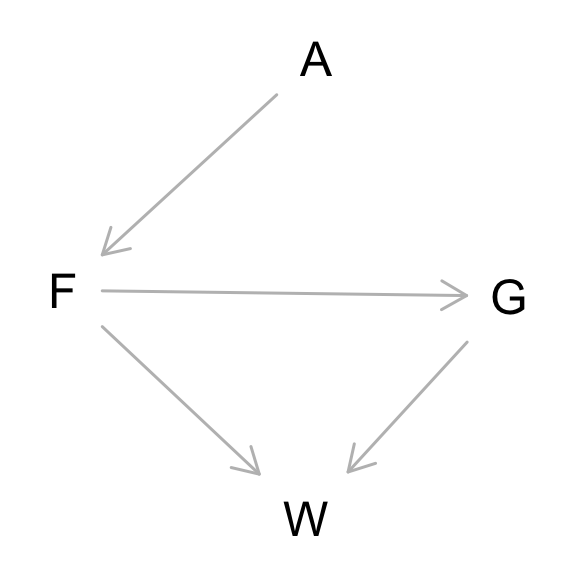
where F is avgfood, G is groupsize, A is area, and W is weight.

Part 1: Use the backdoor criterion and estimate the total causal influence of A on F.

Part 2: What effect would increasing the area of a territory have on the amount of food inside it?

[Write answer here in sentences]

Question 2

Now infer both the total and direct causal effects of adding food F to a territory on the weight W of foxes. Which covariates do you need to adjust for in each case? In light of your estimates from this problem and the previous one, what do you think is going on with these foxes? Feel free to speculate—all that matters is that you justify your speculation.

Question 3

Reconsider the Table 2 Fallacy example (from Lecture 6), this time with an unobserved confound U that influences both smoking S and stroke Y. Here’s the modified DAG:

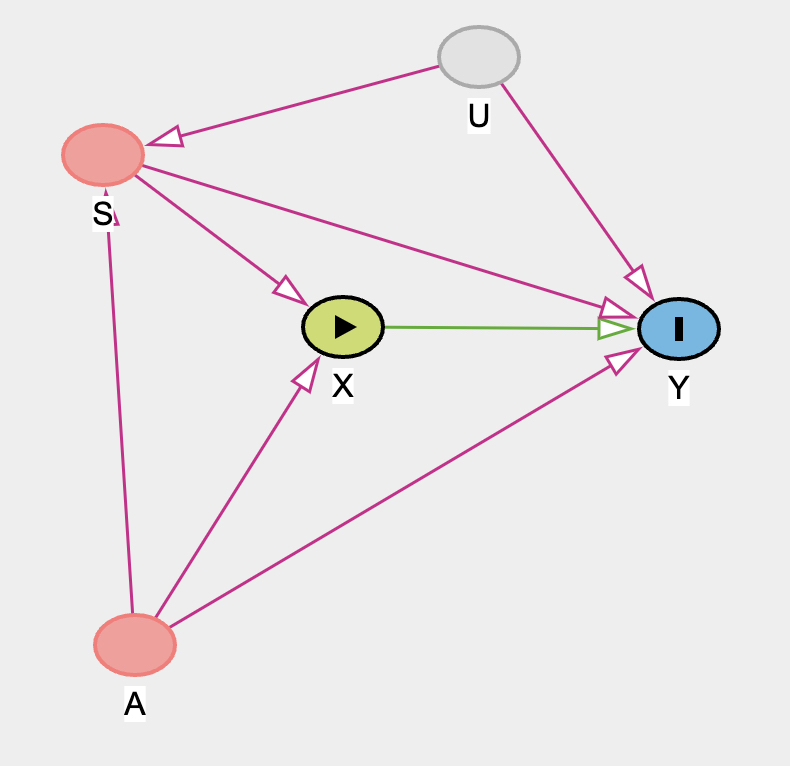
Part 1: use the backdoor criterion to determine an adjustment set that allows you to estimate the causal effect of X on Y, i.e. P(Y|do(X)).

For this exercise, you can use dagitty.net.

Step 1: Input your DAG into Dagitty.net and copy/paste your results here:

# insert code here

g <- dagitty('
          # copy/paste dagitty.net code for DAG here
             ')

Step 2: What is the adjustment set to estimate the causal effect of X on Y?

Part 2: Explain the proper interpretation of each coefficient implied by the regression model that corresponds to the adjustment set. Which coefficients (slopes) are causal and which are not? There is no need to fit any models. Just think through the implications.

[Write answer here in sentences]